-
2026.01.26演習問題 ログサイン積分
-
2026.01.12ランダムウォークの特性関数
-
2025.05.30格子上のランダムウォーク1
-
2025.05.30零除算を許す数の体系
-
2025.05.30いろいろな無限大
PRACTICE PROBLEMS
演習問題
FEATURE ARTICLES
特集記事
-
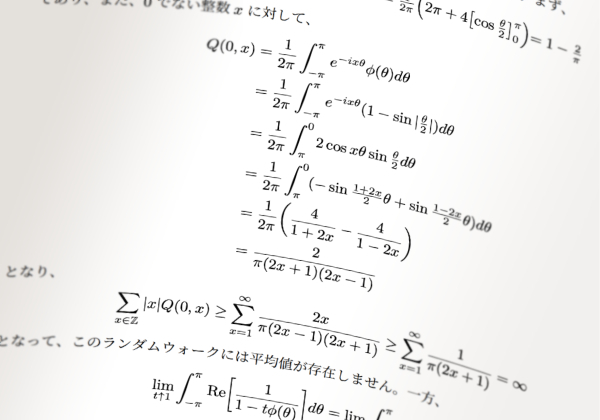 ランダムウォークの特性関数
ランダムウォークの特性関数ランダムウォークの特性関数 仁謹(Jyn kin) 仁謹です。今回は特性関数というものを定義し、三角関数の知識によってランダムウォークの性質を分析していきましょう。 推移関数\(P(x, y)\)によって定まるランダムウォークに関して、半開区間の直積\((-\pi, \pi]^d\)を定義域とする複素数値関数 \[\phi(\theta) := \sum_{x \in R}e^{ix\theta}
-
 格子上のランダムウォーク1
格子上のランダムウォーク1格子上のランダムウォーク1 ~ベルヌーイランダムウォークの再帰性~ 仁謹(Jyn kin) 初めまして仁謹です。いきなりですが、 今回はランダムウォークについてお話します。 特に、格子上のランダムウォーク、つまり、値が固定された自然数\(d\)に対して、 \(d\)次元の格子\(R\)というものを考え、その上を移動する点について考えていきましょう。 \[R := \{x = (x_1, x_2,
-
 零除算を許す数の体系
零除算を許す数の体系「0で割ってはいけません」とよく言われますが,通常の実数や複素数以外の体系で0で割ること(零除算)ができるようなものはいくつかあります.今回はそのような体系の例である実射影直線,輪(wheel),リーマン球面,前草原についてご紹介します. 1 そもそも何故0で割ってはいけないのか? そもそも「0で割ってはいけません」と言われるのは何故でしょうか? このようなことが言われる前提となる文脈では実数や複


